ウェーブレット解析モジュール Unit/Wavelet
Unit/Waveletは、SPLを利用して、ウェーブレット解析のために必要な関数を提供するものです。関数の利用は、メニュー方式で必要な機能を選択すれば、データの解析ができます。 提供されるファイルはテキストファイルですので、必要に応じて自ら改造することもできます。
FFTや、スペクトラム解析では、計測した区間を全体としてとらえるので、その区間内で局所的に存在する波を存在する時間帯を特定して捕らえることは困難です。しかし、連続系ウェーブレット解析では、波の局所的存在を捕らえることができます。
-
Ver3.2 新機能
- 細分型Wavelet(FFT)追加
- 周波数の設定方法についての解説を追加
- 繰り返しの計算の最適化
- DualOrth351(), BurtAdelson() の表示形式変更
-
Unit/Wavelet Ver 2.1
1.モジュール内部のデータ操作を変更し、
FFTを使った連続Waveletの処理速度を10倍程度に向上させました。2.サンプルワークシートを使い易くしました。
3.離散ウェーブレットによる展開を2つ増やしました
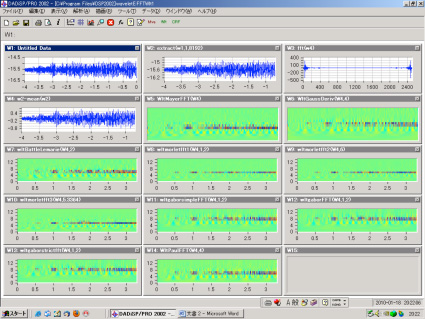
主な機能
連続系ウェーブレット解析
- メキシカンハット
- フレンチハット
- Gabor関数
- Morlet(複素)変換
- B-Spline変換
- Shannonウェーブレット
- Paulウェーブレット変換
- Morlet(Real)変換
- FFTによる連続ウェーブレット変換
- Mayer(FFT)変換
- Gauss微分
- Battle-Lemarieウェーブレット
- Morlet(FFT)変換
- Gabor(FFT)変換
- Paul(FFT)変換
離散ウェーブレット解析
- Hear基底による一次元離散系Wavelet変換
- Haar基底による2次元離散系Wavelet変換
- Daubechies、Coifman(Coiflet)、Baylkin変換
- Symlet変換
- 対称双直交変換
- DualOrth351変換
- BurtAdelson変換
- スペクトル成分
- 近似逆行列
- システム行列
基底読み込み
- Daubchies基底
- Coifman基底
- Baylkin基底
- Symlet基底
- DualOrth基底(351)
- BurtAdelson基底(355)
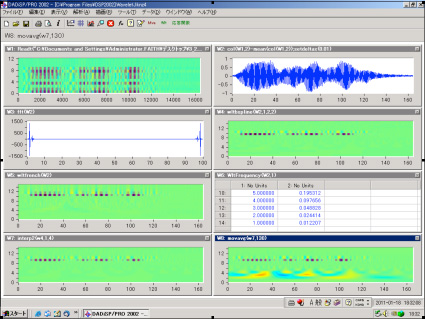
W2では、高周波成分は、時間的に見て後半部分にのみ存在し、前半部分にはありません。 W1は全ての時間帯に渡って高周波成分が存在します。Spectrumでは、この周波数成分の時間的局在性は分かりません。しかし、W4のグラフは後半部分にのみ高周波成分が存在する事がはっきりと表現されています。
ウェーブレット解析の利用について
ウェーブレット解析は、周波数と存在する時間帯の両方を調べるために行列計算が必要であり時間がかかります。FFTの計算結果は1次元データとなりますが、連続系Wavelet解析の結果は2次元データとなるので、計算時間がかかるのです。さらに、Wavelet解析でのデータサイズは必ず2の巾乗でなくてはなりません。1次元データはデータ長が2の巾乗。行列は行数、列数ともに2の巾乗にしてください。このような制限はあるものの、波の局在性を目で見ることができることは分析手段として魅力的でもあります。また、離散系Wavelet解析は近似逆行列の計算やその他の近似理論への応用などもあり、これから様々な利用方法が考えられます。
便利なサンプルワークシート集
Unit/Waveletには、解析例の御紹介を目的としたサンプルワークシート(スプレッドシート)が用意されています。各ウィンドウの解説付きですので、簡単に改良して使用することができます。
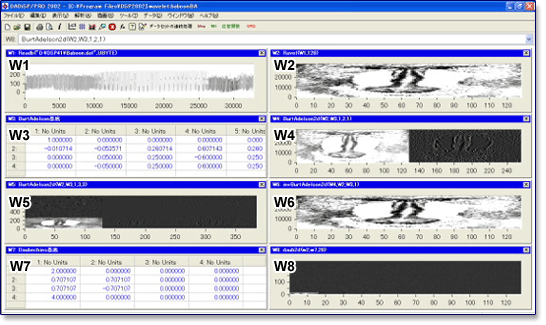
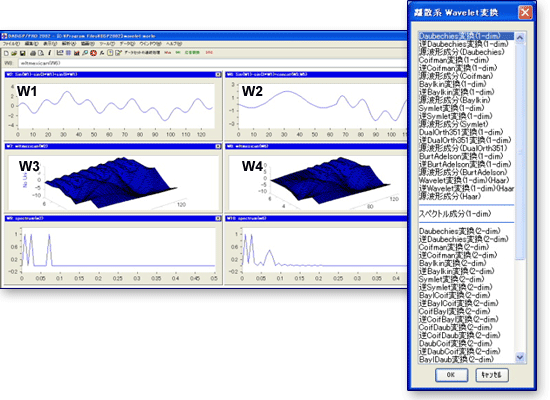
W2が、画像データです。そのウェーブレット2次元元変換W4はBurtAdelson基底を使っています。W6は2次元逆ウェーブレット変換でW2の元データが得られることを確認しています。W8はドビッシー基底での変換です。画像の輪郭を抽出しています。