Analog and Digital Control Module アナログ、ディジタル コントロール モジュール
DADiSP/Controlsは、離散的および連続的線形時間不変量SISO(Single Input/Single output)コントローラーの設計、解析、およびシミュレーションを正確かつ簡単におこなえるモジュールです。それらは、ポップアップ メニューと1行のコマンドで処理されます。
このモジュールには、PIDコントローラーの設計、連続二次システムの瞬時オープン・クローズループ周波数・時間応答の設計、およびラグ・リード補正器の対話的設計を短時間でおこなえるメニューが含まれています。
主な機能
- シンプルなユーザーインターフェース
- 一般的コントローラーを対話的に設計する手法を採用
- インパルス、ステップ、ランプ、および周波数応答計算
- バイ・リニアー、バックフォワード インテグレーション、ゼロオーダー・ホールドモデル
- ボード、ナイキスト、ルートーロカス、およびポール・ゼロ・プロット
- オープンループとクローズループ変換
- PID、PI、およびPD設計
- 遅延素子、ラグ・リード補正器
機能詳細
-
アナログ・ディジタル制御モジュール
DADiSP/ Controlsモジュールは、離散系及び連続系の線形SISO制御器の容易で正確な設計、分析、さらにシミュレーションを可能にします。DADiSP/ Controlsモジュールのすべての機能は、使いやすいポップアップ・メニューか一行のコマンドのいずれかによって利用できます。また、便利なオンライン・ヘルプ・メニュー及び例題が提供されます。
-
迅速かつ容易に制御器の設計ができます
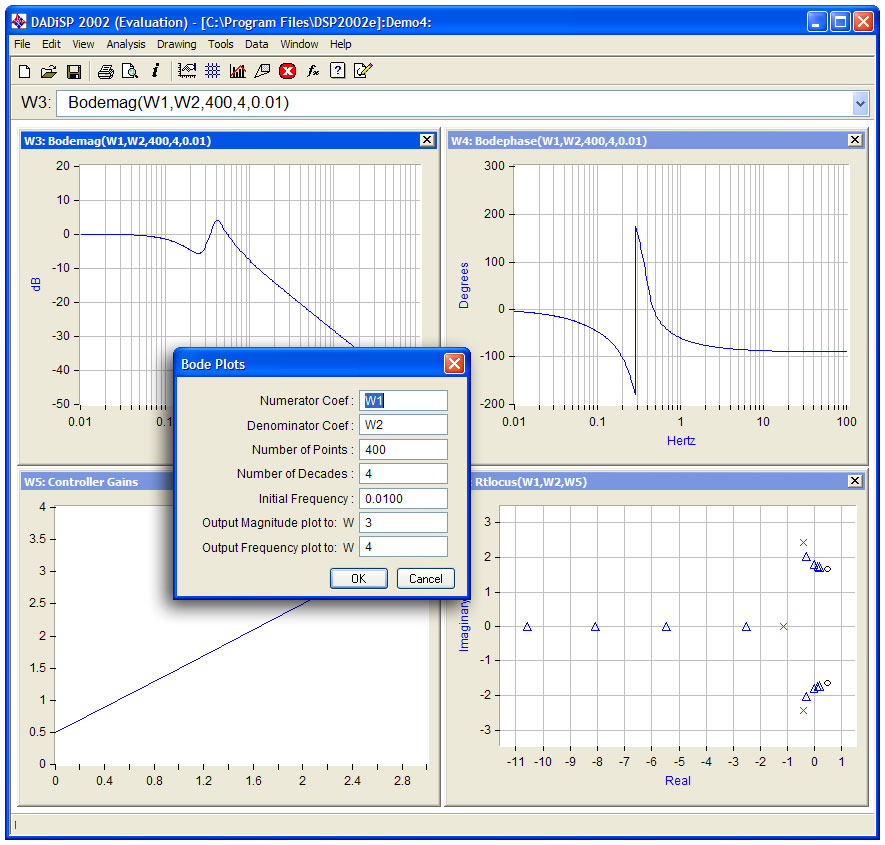
DADiSP/ Controlsモジュールは、DADiSPに完全に統合されて、設計中のモデルがどの様に機能しているかを表示できます。DADiSP/ Controlsモジュールは、一般的な制御器(PID)、連続2次系のオープン・クローズ・ループ周波数・時間応答の設計、ラグ・リード補償器の迅速な設計のためのメニューを提供します。
-
連続系から離散系に、離散系から連続系に変換
DADiSP/ Controlsモジュールは、離散系等価の連続系モデルと連続系等価の離散系モデルを計算する様々な方法を提供します。それらは、ゼロ次・ホールド、Bilinear法(Tustin変換、Trapezoidal rule)、Backward Integration法、あるいは処理遅れのゼロ次ホールド等です。DADiSP/ Controlsモジュールは、指数関数に近似する一次、あるいは二次のPade近似の連続系における遅れをモデル化します。
-
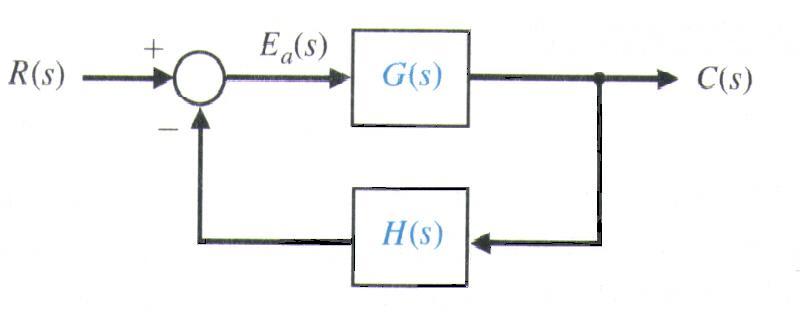
共通システムのインタラクティブな設計
DADiSP/Controlsモジュールは、一般的な制御系(連続系と離散系の位相補償器や二次連続系)のインタラクティブな設計手法を提供します。この方法は、システムの伝達関数の係数及びパフォーマンス特性の仕様によってシステムが設計されることを可能にします。インタラクティブな設計は、システムの支配的な特性を反映し、繰り返し変更されることを可能とする設計メニューを使用することによって可能になります。設計中の各段階では、最新の修正点の反映、そしてシステムのすべての特性が再計算されます。全システムが、設計仕様を満足した場合に限り、係数の出力が指定のウィンドウに出力されます。
-
初期条件を備えたシミュレーション
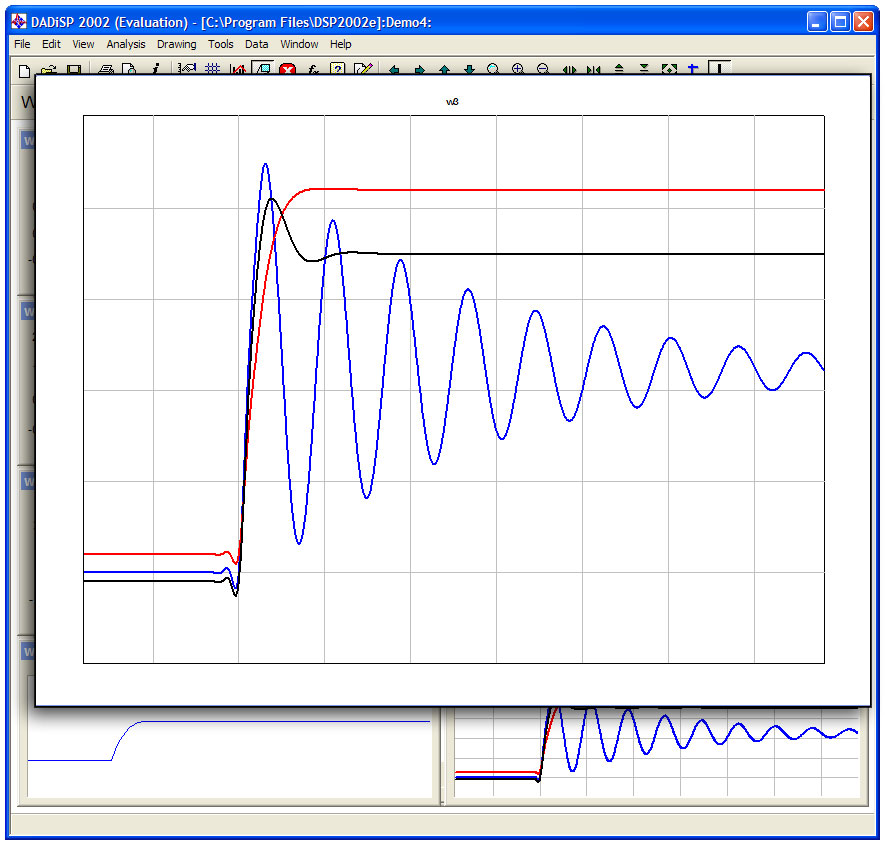
DADiSP/Controlsモジュールは、初期条件を備えた連続系のシミュレーションの開発のために、微分方程式にState Space Realization、及びEigenvector法を使用しています。また、例題には、この種のシミュレーションを開発するために、どの関数を使用すべきか、また適切な手順は何かの説明がなされています。
DADiSP/Controls
DADiSP/ Controlsモジュールは、40以上の関数を持っています。以下にその要約を示します。
解析とシミュレーション
| bode | Bodeゲイン線図と位相線図をプロット |
|---|---|
| nyquist | ナイキスト線図をプロット |
| fstats | Bode線図から周波数応答特性を計算 |
| dbode | 離散系のBode線図を計算 |
| dnyquist | 離散系のナイキスト線図を計算 |
| dfstats | 離散系のナイキスト線図から周波数応答特性を計算 |
| setfunit | 周波数応答マクロで使われる単位を設定 |
| pzmap | 複素平面中のポールとゼロの位置をプロット |
| rtlocus | ルート・ローカス(Root Locus)・プロット |
| pzgrid | 一定の固有周波数と減衰比のグリッドを重ねてプロット |
| dpzmap | 離散系のポールとゼロの位置をプロット |
| drtlocus | 離散系のルート・ローカス(Root Locus)・プロットを計算 |
| dpzgrid | 2次離散系の一定の固有周波数と減衰比のグリッドを重ねてプロット |
| cimpulse | 連続系のインパルス応答を計算 |
| cstep | 連続系のステップ応答を評価 |
| cramp | ランプ入力に対する連続系の応答を計算 |
| csim | 指定された入力に対する連続系の応答を計算 |
| csiminit | 指定された入力と初期条件に対する連続系の応答を計算 |
| dimpulse | 離散系のインパルス応答を計算 |
| dstep | 離散系のステップ応答を評価 |
| dramp | ランプ入力に対する離散系の応答を計算 |
| dsim | 指定された入力に対する離散系の応答を計算 |
| dsiminit | 指定された入力と初期条件に対する離散系の応答を計算 |
| tstats | 連続系又は離散系のステップ応答プロットからパフォーマンス特性を計算 |
モデルの変換
| connect | 2つのモデルを一つのモデルに結合 |
|---|---|
| cloop | 開ループ・モデルを閉ループの変換 |
| cloopf | 開ループかつフィードバック伝達関数から閉ループ伝達関数を生成 |
| delay | 連続系で簡単な近似の遅れをモデル化 |
| delay2 | 連続系で高次の近似で遅れをモデル化 |
| c2disc | 連続系伝達関数のゼロ次ホールドを持つZ変換によって離散系伝達関数を計算 |
| c2dbil ? |
バイリニアー(bilinear)変換により連続系伝達関数の等価離散系伝達関数を計算 |
| c2dback ? |
Backward Integration法により続伝系達関数の等価離散系伝達関数を計算 |
| c2ddelay | 処理遅延を持つ連続系伝達関数でゼロ次ホールドを持つZ変換を実行 |
| dcgain | 連続系のDCゲインを計算 |
| cresolv | 連続系のResolvantマトリックスを計算 |
| d2cont | 連続モデルを生成するためにゼロ次ホールドを持つ逆Z変換を実行 |
| d2cbil | Bilinear変換の逆変換を使って離散系伝達関数を等価連続系モデルにする |
| d2cback | Backward integration法の逆変換を使って離散系伝達関数を等価連続系モデルにする |
既製の制御器の設計
| connect | 2つのモデルを一つのモデルに結合 |
|---|---|
| cloop | |
| pid | PID制御器の設計 |
| pi | PI制御器の設計 |
| pd | PD制御器の設計 |
| lagleadm | ラグ・リード補償器の設計 |
| dpid | 離散系PID制御器の設計 |
| dpi | 離散系PI制御器の設計 |
| dpd | 離散系PD制御補償器の設計 |
| dlagleadm | 連続系等価の離散系リード・遅延器の設計 |
| dsgn2ordm | 2次連続系の設計 |